Project Context

This project involved numerical simulation of 2D incompressible flow in a square lid-driven cavity using the vorticity–stream function formulation. The problem served as a benchmark CFD case to validate numerical implementation, boundary conditions, and solver behavior.

Engineering Problem

• Obtain a physically correct solution for lid-driven cavity flow

• Correct improper enforcement of top-wall velocity boundary conditions

• Ensure stable convergence of the coupled vorticity–stream function equations

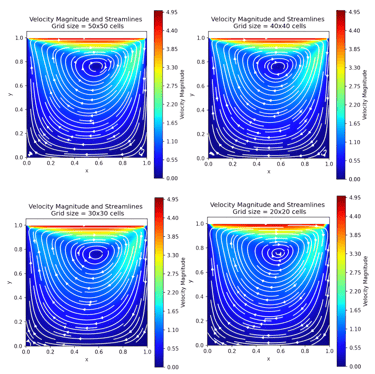
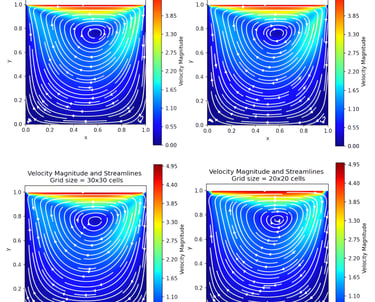
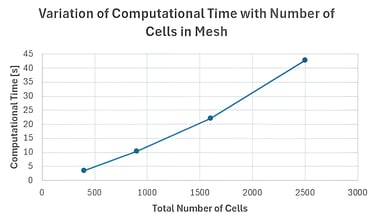
• Study the impact of flow velocity and mesh resolution on accuracy and runtime

Approach & Methodology

The governing vorticity transport and Poisson stream-function equations were discretized using finite differences and implemented in Python. A Successive Over-Relaxation (SOR) scheme was used to solve the stream-function equation at each time step. Boundary conditions for vorticity and stream function were analytically derived and explicitly enforced at all walls, with special treatment of the moving lid. Velocity components were computed from the stream function using central differencing. Parametric studies were performed by varying top-wall velocity and mesh resolution, with convergence and CFL stability monitored.

Key Results

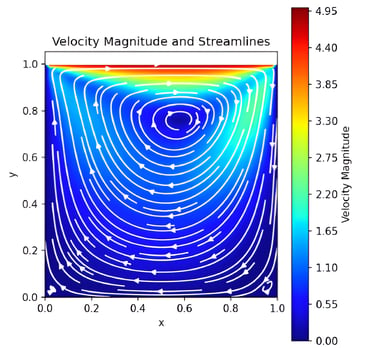
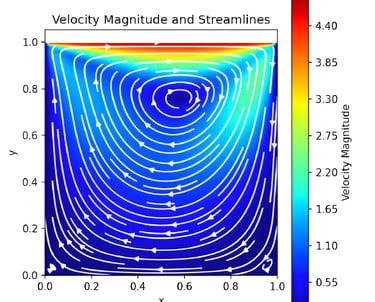
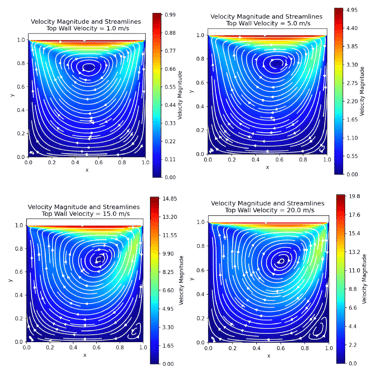
• Correct enforcement of boundary conditions restored the prescribed top-wall velocity and eliminated unphysical zero-velocity behavior

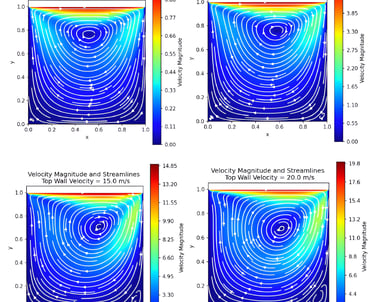
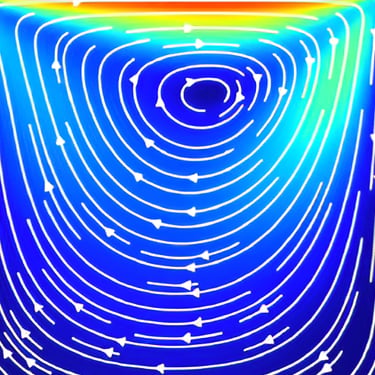
• Formation of a primary central vortex with secondary corner recirculation zones observed at steady state

• Increasing lid velocity (1–20 m/s) intensified circulation and shifted the primary vortex toward the downstream side

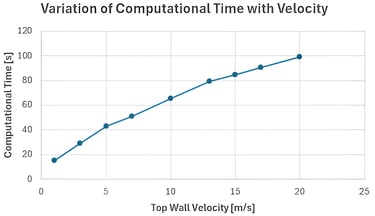
• Computational time increased approximately linearly with lid velocity due to slower SOR convergence

• Simulations became unstable beyond ~20 m/s due to CFL condition violation

• Mesh refinement improved resolution of secondary vortices but caused a sharp increase in computational time

Engineering Judgment & Trade-offs

Explicit boundary treatment improved physical accuracy but required careful handling of wall vorticity expressions. Higher lid velocities and finer meshes improved flow resolution at the cost of numerical stability and runtime. The study highlighted the trade-off between computational efficiency and fidelity in explicit time-marching CFD solvers.

Tools & Methods

Python, NumPy, Matplotlib, finite-difference discretization, vorticity–stream function formulation, SOR iterative solver.

Outcome / Takeaway

The project delivered a corrected and validated CFD implementation for a classical benchmark flow. It demonstrated strong understanding of boundary-condition enforcement, numerical stability limits, and resolution–cost trade-offs in incompressible CFD.